Zeta space as a probabilistic model

Consider $ S^n,$ the space of Schur-convex, simply connected, closed topological $n-$manifolds as subsets of the unit $(n+1)-$cube, which include $p=(0,0,\cdot\cdot\cdot,0)$ and $q=(1,1,\cdot\cdot\cdot,1).$ Consider the set of all Schur-convexity preserving maps from $S^n$ to itself.


Define a class of $S^n,$ denoted $\zeta(\mathbf X),$ in the following way:


Let $ L^n_+$ be the set of all $n$-dimensional nonnegative random vectors $\mathbf X = (X_1, X_2,\cdot\cdot\cdot,X_n)^⊤$ with finite and positive marginal expectations, and let $\mathbf Ψ^{(n)}$ be the class of all measurable functions from $\Bbb R^n_+$ to $[0, 1].$ Then $\zeta(\mathbf X)$ of the random vector $\mathbf X$ with joint CDF $F$ is:


$$\zeta(\mathbf X)=\bigg\{\bigg(\int \psi(\mathbf x)dF(\mathbf x), \int \frac{x_1\psi(\mathbf x)}{E(X_1)}dF(\mathbf x),\cdot\cdot\cdot,\int \frac{x_n\psi(\mathbf x)}{E(X_n)}dF(\mathbf x):\psi \in \mathbf Ψ^{(n)}\bigg)\bigg\}, $$


$$ =\bigg\{\bigg(E\psi(\mathbf X), \frac{E(X_1\psi(\mathbf X))}{E(X_1)},\cdot\cdot\cdot,\frac{E(X_n\psi(\mathbf X))}{E(X_n)}:\psi \in \mathbf Ψ^{(n)}\bigg)\bigg\}. $$


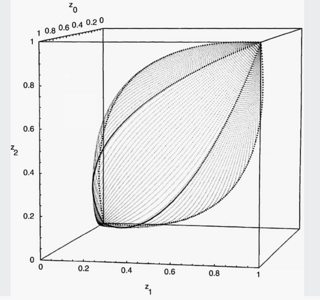
Let me provide a concrete example. I have a 3D graph of $\zeta$ for a bivariate II Pareto distribution with parameters $(\mu_1,\mu_2,\sigma_1,\sigma_2)=(0,0,1,1)$ and $\alpha=9$ so I know the qualitative nature of the shape of any given surface given by any distribution. Here is a picture to give some intuition about the definition:





I was interested in obtaining the volume for $\zeta(\mathbf X).$ I calculated it to be:


$$\mathrm{Vol}(\zeta(\mathbf X))= \frac{1}{(n+1)!}E\big(|\det(Q)|\big). $$


where $Q$ is a $(n+1)\times(n+1)$ matrix whose $i$th row is $(1, \mathbf{ \bar X}^{(i)}),$ $i=1,2,\cdot\cdot\cdot , n+1.$


Here I'll use a normalized version of $\mathbf X$ denoted by $\mathbf{\bar X}$ such that $\bar X_i= X_i/E(X_i),$ $i=1,2,\cdot\cdot\cdot, n.$ Consider $n+1$ $\mathrm{iid}$ $n$-dim. random vectors $\mathbf{ \bar X}^{(1)},\cdot\cdot\cdot, \mathbf{ \bar X}^{(n+1)} $ each with the same distribution as $\mathbf{\bar X}.$ 


I was interested in the Mellin transform of the volume form of $\zeta$ which can be written as:


$$ \Pi_n(s)=\int_{\zeta} x^{s} ~\mathrm{Vol}(\zeta(\mathbf X)) \frac{dx}{x} $$


The reason for investigating this object is to construct a symmetrical completion of $\zeta(\mathbf X)$ in the sense that $\zeta(\mathbf X)$ is just one component in the space. We can add three more of these components to obtain $\zeta_{\mathrm{complete}}.$





Then one can take Mellin transforms of the volume forms on each of the components, paying particular attention to how the mutual intersection volume region transforms into the image space under the Mellin transform. Call this region $R$ which is a subset of $\Bbb C$.


> What can be said about $R$?


Comments

Post a Comment

Popular posts from this blog

Automorphisms and zeta space

Image
Here I will operate under the assumption that $\phi_s$ is a unique and well-posed solution to the following PDE. This means whatever conditions are needed for that to occur, will be imposed. $$s\frac{\partial^2}{\partial s^2}\phi_s(x)=\mp x\frac{\partial}{\partial x}\phi_s(x) $$ for which we have our pre-assigned unique solution: $$\mathcal \phi_{s}:=\bigg\lbrace e^{\frac{\pm s}{\log x}}:s \in \Bbb R \bigg\rbrace$$ We have singularities at $s=0$ and $x=0,1$ and this will be called a "cross singularity" or  $CS$. A natural idea would be to intialize some distribution on this $CS$ and run time forward giving a wellposed analytic solution for all time. So we choose our pre-assigned solution $\phi_s$ and run the solution back in time where we obtain what we wanted, at least qualitatively. We can throw out our solution for $s<0$ because it doesn't directly apply to the situation, and it does not rapidly decay. Meanwhile, for $s>0$ it is Schwartz i.e. has a rapid decay cr
Read more

Gluing leaves in zeta space and automorphisms on the resulting quotient spaces

Define an analytic planar homotopy $h_t: (0,1) \to (0,1)$ for $t\in[1/3,3]$ where $h_t(x)=e^{\frac{t}{\log x}}$ s.t. $h_{1/3}=e^{\frac{1/3}{\log x}}$ and $h_3=e^{\frac{3}{\log x}}$ for $x\in(0,1)$. I want a rotational homotopy that projects onto the planar homotopy. So, define the equivalence relation on the boundary curves of the closed subset of $(0,1)^2$, that is $h_{1/3}\sim h_3$, where points are identified by straight lines with slope $1$, connecting $h_{1/3}$ and $h_3$. This yields a spherical topology $\mathcal S$ embedded in $(0,1)^3$ with the endpoints of the sphere being singularities at $p=(0,1,1)$ and $q=(1,0,0)$.  Conceptually it's clear that a projection $\pi: (0,1)^3 \to (0,1)^2$ takes the leaves on $\mathcal S$ to $h_t(x)$ as a double cover. But my main objective of study is to put a metric on $\mathcal S$. The $1$-parameter metric I derived on the planar space is $g_t(r)=\int_{(0,1)} x^{r-1}h_t(x)~dx = 2\sqrt{\frac{t}{r}}K_1(2\sqrt{tr})$ and it measures the distan
Read more

Representation of Zeta space from a PDE and combinatorial viewpoint

Image
Consider the following partial differential equation: $$ s \frac{\partial^2}{\partial s^2} \phi(x,s) = - x \frac{\partial}{\partial x} \phi(x,s) $$  with our classical analytic generator as in the previous post, $\phi_s(x)=e^{\frac{s}{\log x}}$. This local foliation generates zeta space on the base planar space.  Now, each leaf of the foliation directly corresponds to a Schwartz function therefore we can build out corresponding symmetric function equations and gather critical strips for each leaf. The goal going forward will be to establish a very particular generalization of the leaves on the base space and allow them to sit in $\Bbb R^3$. They will form football like structures and the football structures can be seen as sections sitting over top of the base space. In fact, the base space of the foliation will be pasted onto each "face" of the corresponding cube, wherein the football structures will be promoted within the cube. Then we will study the combinatorics of zeta sp
Read more