A Four-Sheeted Orbifold Foam as a Planck-Cell Carrier

-
 One possible way to think about Planck-scale structure is not to begin with a smooth spacetime manifold, but with a finite geometric carrier on which quantum data can be placed. In this note I describe a speculative mathematical object of this kind: a four-sheeted football-orbifold foam suspended over the face poset of a cube. The proposal is not that ordinary spacetime literally contains small Euclidean cubes. Rather, the cube poset should be understood as a finite incidence scaffold: it records which zero, one, two, and three-dimensional strata are allowed to meet, while the actual geometric realization is an orbifold/Klein foam built over that combinatorial skeleton.  Let $P_{\Box}$ denote the face poset of a cube. The eight vertices of the cube serve as incidence markers for the eight cone points of the foam. Since a football orbifold has two cone points, one can naturally attach four football sheets by pairing the eight vertices into four antipodal pairs. Thus we begin w...
Post a Comment

Automorphisms and zeta space

-

Here I will operate under the assumption that $\phi_s$ is a unique and well-posed solution to the following PDE. This means whatever conditions are needed for that to occur, will be imposed.


$$s\frac{\partial^2}{\partial s^2}\phi_s(x)=\mp x\frac{\partial}{\partial x}\phi_s(x) $$

for which we have our pre-assigned unique solution:

$$\mathcal \phi_{s}:=\bigg\lbrace e^{\frac{\pm s}{\log x}}:s \in \Bbb R \bigg\rbrace$$

We have singularities at $s=0$ and $x=0,1$ and this will be called a "cross singularity" or  $CS$. A natural idea would be to intialize some distribution on this $CS$ and run time forward giving a wellposed analytic solution for all time. So we choose our pre-assigned solution $\phi_s$ and run the solution back in time where we obtain what we wanted, at least qualitatively.

We can throw out our solution for $s<0$ because it doesn't directly apply to the situation, and it does not rapidly decay. Meanwhile, for $s>0$ it is Schwartz i.e. has a rapid decay criterion, and we know its Mellin transform exists and has a closed Bessel form. This will be employed to extract a *1-parameter family* of functional equations for the Riemann zeta function.

$$\Gamma(\phi,r,s)\cdot \zeta(s) = \Gamma(\hat{\phi},r,1-s)\cdot \zeta(1-s)$$

whereby moving $\zeta(s)$ to the RHS gives us a partial differential relation on the factor $\Gamma(\phi_s,r)$

$$r^2 \frac{\partial ^3}{\partial r^3}\Gamma(\phi_s,r) =s^2 \frac{\partial}{\partial s}\Gamma(\phi_s,r) $$

where we recognize that the Mellin transform of our Schwartz family, $\phi_s$ must obey a third order (shallow water wave) PDE. Here we explicitly calculate the factor which we can quickly verify as a solution.

$$\Gamma(\phi,r,s)=\int_{\mathbb R^\times \cap ~(0,1)} |x|^r~\phi_s(x)~{dx\over |x|}=2 \sqrt{\frac{s}{r}}K_1(2\sqrt{r s})$$

My motivation at least, stems from building a space, a so called zeta-space, or $\zeta$-space which somehow encodes all of what I wrote above and goes further, letting one express automorphisms of $\zeta$-space as leaving critical strips invariant under these automorphisms. 

I will now transition to more visual diagrams in part because it's much easier to convey the point and because I am much less sure how to rigorously show the mathematics in this part of the post.

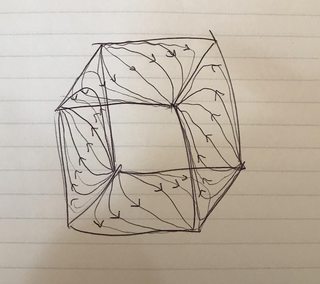
$\phi_s$ is now shown to be decorated on all the panels of the unit cube in $\Bbb R^3$. I left out two panels because it would get cluttered. Here $\phi_s$ are understood to be our $1$-parameter family of Schwartz functions (the solutions we did not discard from the original 2nd order PDE).






We can build sections within the cube by gluing bounded subsets of the $\phi_s$ solutions to the original 2nd order PDE and requiring (by definition of a section) that projections take us onto the leaves, $\phi_s$ on the base space. If we do this correctly, the sections should look like this:






Finally we symmetrize to get symmetrical $\zeta$-space:





This is not rigorously posed yet because I haven't figured out how to say it precisely, but if the 3 rubber band loops around the object allow the object to act like a Rubiks cube group we can get a permutation structure on zeta-space. Any Rubiks cube transformation leaves the boundary invariant i.e. leaves the Schwartz families unchanged corresponding to an invariant quantity of the automorphisms of zeta-space.




Comments

Post a Comment

Popular posts from this blog

The "Seed" $\mathcal S = (\mathcal I, \Gamma, \Pi)$

-
Image
Consider a triple $\mathcal S = (\mathcal I, \Gamma, \Pi)$, where $\mathcal I$ is a compactified 4-sheeted branched cover of $\Bbb C$, $\Gamma \subset \mathcal I$ is a constellation (D'essin D'enfant in simpler cases), and $\Pi$ is a finite nonabelian piecewise isometry group. Specifically, let $\mathcal{O}_1, \dots, \mathcal{O}_4$ be four spindle orbifolds (topologically, Riemann spheres $\widehat{\mathbb{C}}$ each with two cone points). Let their union form the 2-complex: $$\mathcal{I} = \bigcup_{j=1}^{4} \mathcal{O}_j$$ These four surfaces intersect precisely along a 1-dimensional locus $\Gamma$, which serves as the 1-skeleton of the complex. Combinatorially, $\Gamma$ is a 4-regular octahedral graph ($|V| = 6$, $|E| = 12$). Geometrically, $\mathcal{I}$ is intrinsically parameterized within a bounding 3-dimensional cube, with the $6$ vertices (0-cells) of $\Gamma$ sinking into the interior, located exactly on the local coordinate planes $x, y, z = 1/2$. Let $P = \{p_{j,1}, p_...
Read more

The Canonical Construction of $\mathcal I$ Using Differential Geometry

-
Image
We will construct a highly symmetric leaf (an interface leaf) as a special subset in some $\mathcal F$-completion, this time furnishing the leaf with additional geometric data including a metric and curvature. We start by asking the following optimization question: Fix $n=3$ and consider a surface of revolution $S$ and an embedding $e:S \hookrightarrow X^3$ for $X^3=[0,1]^3$ with points $p,q$ elements of $\partial X^3$ where $\partial X^3=X^3-(0,1)^3$ for $\mathrm {sup}~ \mathrm{dist}(p,q)=\sqrt{3}$.    What is $\rho_{\mathrm{max}}=\mathrm{max} \lbrace \mathrm{vol}(S) \rbrace_{p,q}$ assuming $S$ must remain a surface of revolution and have constant positive Gaussian curvature? An abstract surface of revolution with constant positive Gaussian curvature (to be embedded/optimized) within $X^3.$ In other words, what is the volume of the largest surface of revolution with constant Gaussian curvature that can be embedded in $X^3$ with a pair of antipodal corners as cone points? Let ...
Read more

The Spectral Hermitian Surface $(\Bbb C^\times, g_{\infty})$ as an Avatar of a Modular Surface

-
Consider $\mathcal F=\lbrace \mathcal L_t=(\Bbb C^{\times},g_t(s)) \rbrace_{t\in\Bbb R_{\gt 0}}$ where $g_t(s)=\vert F_t(s) \vert^2ds\otimes d\bar{s}$ and $$F_t(s)=\int_{(0,1)} e^{t^2/\log x} \cdot x^{s-1}dx= 2\sqrt{\frac{t^2}{s}}K_1(2\sqrt{t^2s}). $$ For $K_1$ the modified bessel function of the second kind. Looking at Bessel asymptotics we know that as $s\to 0$, $g_t(s)\sim \frac{1}{|s|^2}ds\otimes d\bar{s}$ (conical) and as $s\to\infty$, $g_t(s)\sim e^{-4\sqrt{t^2s}}ds\otimes d\bar{s}$ (collapsing end), and these asymptotics hold for the later defined $g_{\infty}(s).$  Define a trace over $F_t$ $$\mathcal M(s)=\sum_{t=1}^\infty F_t(s)$$ then the following identity is satisfied   $$\frac{1+2\mathcal M(s)}{1+2\mathcal M(1/s)}= s^{\alpha}$$ where $\alpha$ is the weight. The proof that there exists some $\alpha \in \Bbb R$ such that the identity holds for all $s$ uses Poisson summation.  Define a new metric which encodes the cumulative effect of the metrics on each of...
Read more